- 2020.09.09
- 採用担当ピックアップ集
連立方程式 基礎の基礎☆

みなさまこんにちは☆
【CADのプロフェッショナル集団】ダイテックスの教育担当です。
9月になりましたが関東では、まだまだ暑い日が続いています。
引き続き熱中症には注意が必要ですね。
さて、以前ブログでもご紹介しましたが、ダイテックスの新入社員研修には、
「設計計算」があります。
新入社員には、計算すること自体久し振り、という人もいたりして
初めは少し苦戦する様子が見られることもあります。
具体的には、単位の変換や、公式変形に戸惑っているように感じます。
そこで、今回はこういった計算系の基礎がぎゅっとつまった
「連立方程式」に触れておきたいと思います。
みなさん、「連立方程式」覚えていますか?
大人の方はもしかしたらその言葉自体、久し振りに聞くという方も
いらっしゃるかもしれませんね。
大抵の人は最初、中学校の数学で習ったかと思います。
「だったらもうそんなの使わないでしょー」と思うかもしれませんが、
ちょっと待ってください!実はそんなことはないのです!
連立方程式は力学にも関係するベクトルや、強度などにも役立つ三角関数、
微分・積分など、様々な問題に絡んできます。
連立方程式が解けないと、これらの問題も自動的に解けません。
つまり、数学のほとんどの問題 + 力学が解けない、ということになってしまうのです。
怖いですね?(ちょっと無理やりでしょうか(笑))
まあ知っておいて損はありませんので簡単に復習(?)していきましょう。
まずよくある易しい文章問題にて。
こういう問題だと、りんごとみかん、鉛筆とノート、などが定番ですよね。
では定番に則って・・・
ある日かほさんは、お店に行って1個120円のりんごと1個80円のみかんを
合わせて8個買った。すると代金は760円だった。
かほさんは、りんごとみかんをそれぞれ何個ずつ買ったか。

文章問題では、式を立てる際、何をxやyなどの文字として置くのか、
がポイントになります。易しい問題であれば、求めたいものをそのまま文字で
置き換えると、式を作るのも計算するのも簡単です。
今回の問題では、りんごの個数をx、みかんの個数をyと置くと簡単でしょう。
そこから与えられている情報を当てはめて式を組んでいきます。
まず、合計の個数が8個ということで
x(←りんごの個数)+ y(←みかんの個数)=8(←全体の個数)
次に全体の金額と、1個ずつの値段が与えられていますので、
120x(←りんごx個の値段) + 80y(←みかんy個の値段) = 760(←全体の値段)
この式を連立方程式にします。
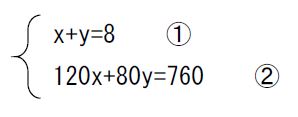
x+y=8 ①
120x+80y=760 ②
解き方はいくつかありますが、今回は代入法でご紹介しますね。
まず、今回はxから求めることにします。
りんごが何個か、というところですね。
ですので、①の式を変形して、
y = 8 – x とします。 xの前に – が付いたのは、
移項(=の向こう側に行くこと)をすると符号が変わる、というルールのためです。
次に、②の式に今の式を適用していきます。
yが8 – xということなので、代入(その文字の代わりに入れること)をします。
すると、②の式から120 x + 80(8 – x) = 760という式を得ることができます。
これを計算します。( )の前の数字は( )の中の項にそれぞれ
掛ける必要があります。
120 x + 80 × 8 + 80 × – x = 760 (足し算引き算より掛け算を先にします)
120 x + 640 – 80 x = 760 ( + × – は – になるのも計算のルールです)
120 x – 80 x = 760 – 640
40 x = 120
x = 3
これでりんごは3個だった、ということがわかりました。
ここからみかんの個数を出しますが、
できるだけ簡単に出せそうな方へ代入します。
②を選んでしまうと計算が複雑になるので、①の式を使いましょう。
x + y = 8 →これを変形します。
y = 8- x → x は 先ほどの計算で3と出たので代入します。
y = 8 – 3
y = 5
以上より、りんご3個、みかん5個 が答えです。
一応検算すると良いですね。
120 × 3 + 80 × 5 これを計算して、 360 + 400 = 760
②の式とも矛盾しませんので問題ないでしょう、という判断ができます。
以上ですが、文章で書くとすごく長くなってしまいますね・・・
今回取り扱ったのは、とても基礎的なものだったので、
そんなのわかるし、どこで使うんだ?と思った方もいらっしゃるかもしれません。
しかし他にも速さや濃度、割引率と定価の問題などなど、
応用問題には結構、実生活に役立ちそうなものがあります。
もし興味を持っていただけた方がいらっしゃいましたら、
復習してみると、意外と面白いかもしれませんよ★
